
「九九がなかなか覚えられない。」「暗算ができない。」「計算手順を理解できない/忘れてしまう。」
そのような学習の入力に凸凹がある子どもは、学校のクラスの中に1~3割程度はいます。その子どもがLDと診断されるレベルであるかはともかくとして、目の前に困っている子どもがいれば、何とかしたいと思う人が多いはずです。
筆者は元小学校教師です。10年間の教員生活の中で、たくさんの「算数が苦手」と訴える子どもたちを教えてきました。
そのような子どもたちに、1年間の中で、LDにも対応し得る様々な教え方を試行錯誤で行ってきました。結果的に95%以上の子どもたちが、テストの点が向上し、教える前よりも算数ができるようになっていきました。
5%の子どもに関しては本当に伸びたのかが懐疑的な部分があります。その5%の中には、IQが70未満の軽度知的障害の子どもたちが含めれています。
現在勤めている発達児童支援の療育施設でも、1~2時間教えた程度で、「先生に教えてもらったら、今まで0点だったのが、いきなり50点取れた。」と子どもから報告を受けています。
LD、またはそうではなくても、算数に苦手意識をもつ子どもたちに効果的な指導方法というものは、確かに存在します。その方法は子どもによって千差万別ですが、大きな原則は変わりません。
今回の記事では、算数を理解する能力のメカニズムと、効果的な指導方法を紹介していきます。これらの方法を試せば、現状から一歩改善、前進できる可能性は大いにあると言えます。
算数LD(ディスカリキュア)の定義
LDの中でも、特に、算数に関して入力、表出の問題を抱える症状をディスカリキュアと言ったりします。ディスカリキュアは主に、2種類の困難を抱えています。それは「数字の概念、数値、または計算を習得することの困難さ」と「数学的推論の困難さ」です。簡単に言えば、計算と文章題です。ディスカリキュアは、図形問題は含まないというところが混同しやすいポイントとなるでしょう。
算数を理解するための4つの力
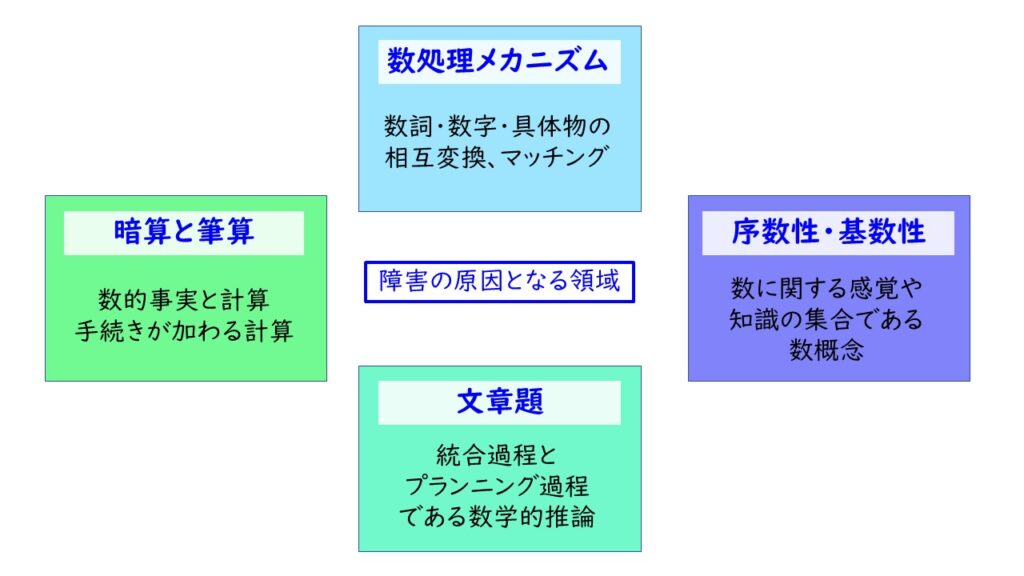
「算数」という教科、学習をを支える4つの力があります。それは「数処理メカニズム」「序数性・基数性」「暗算と筆算」「文章題」の4つです。子どもの力を分析する上でこれらの力の理解が大切になってきます。
数処理メカニズム
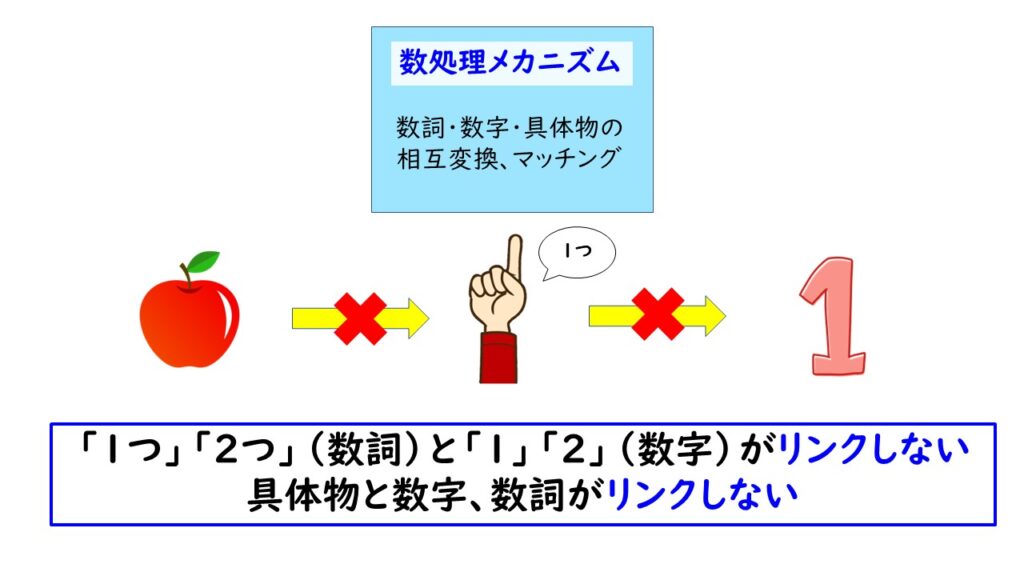
「数処理メカニズム」は、基本的に「一対一対応」のことです。
人間は幼児から成長していく過程で、まず具体物を「1」「2」と数えることを覚えます。そして、その数字は、「1つ」「2つ」という数詞に変換できるようになっていきます。就学後の1年生からは、「カエルが5匹いる→5つのブロックを置く」という具体物を半具体物に変換する過程を経て、数字に変換する工程を踏むようになっているのです。
序数性・基数性
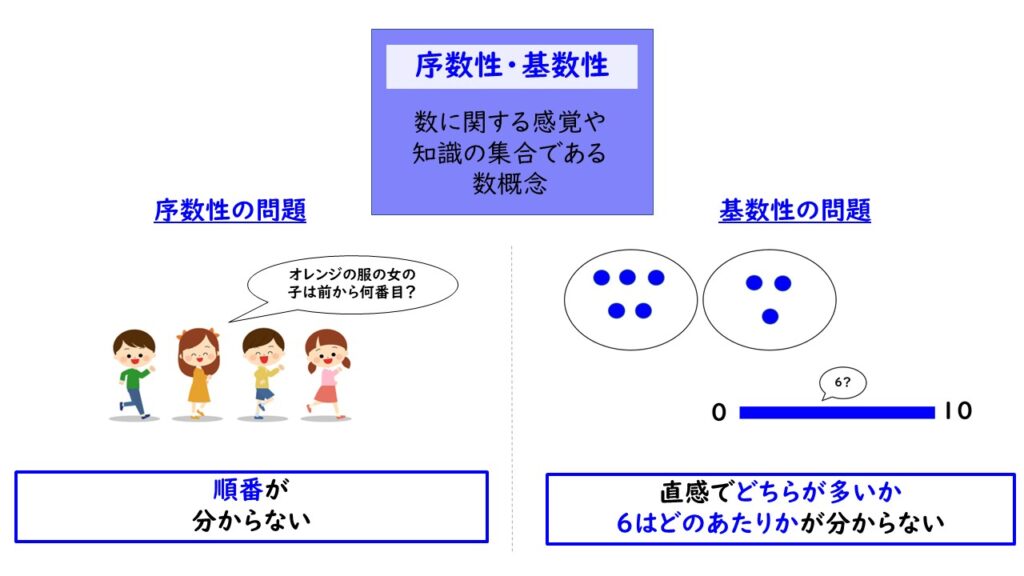
「序数性・基数性」は数の概念を表します。簡単に言えば「順番」と「量感」です。この両者が分からなければ、算数の勉強を進めていても、順序が混乱したり、答えのおおよその見当をつけることに困難を覚えたりすることは明白です。
他にも「モノの集合は左右どちらから数えても全体数の変化はない原理」である「順序無関連」や「数えるものがりんごやみかんなど異なるものでも関係がない」という「抽象性」の原理も数の概念に含まれます。
暗算と筆算
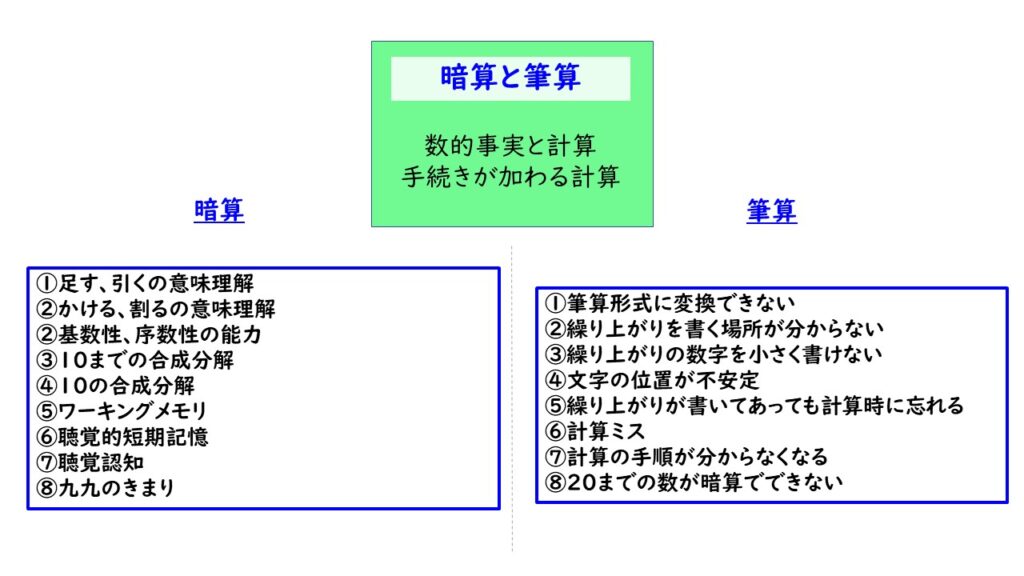
暗算と筆算に困難さを抱えることが多いのが、ディスカリキュアの大きな特徴です。この2つに困難を抱えれば、様々な計算処理でつまずきを覚えることが推測できると思います。
暗算は、1年生からの数に対する理解が積み上がっていく中で、できるようになっていく能力です。ただ、先に述べた「数処理メカニズム」や「序数性・基数性」といった数概念に凸凹を抱えていれば、意味理解ができない学習が積み重なります。その結果、暗算に困難を抱えるという状態が生まれるのです。
また、筆算は、空間認知、計算の手順の問題が浮上してきます。「どこに何を書けばよいのかが分からない」「たてる、かけるの次は何をすればよいかが分からない」といった問題です。
そして両者に共通して大きく関わってくるのは、ワーキングメモリの問題でしょう。一時的に記憶を保持できる情報量の問題、長期記憶から瞬間的に必要な情報を引き出す速度の問題があります。
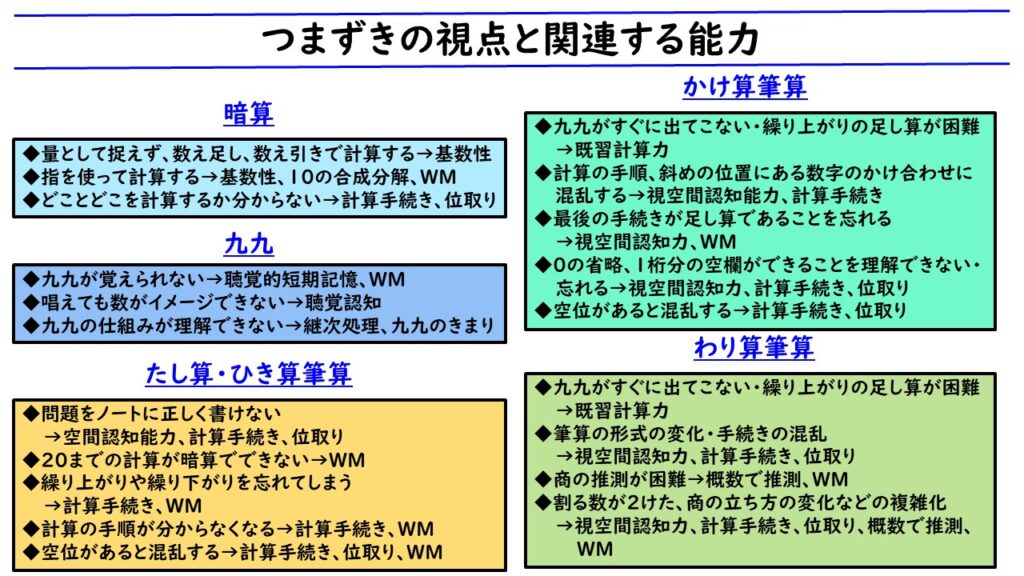
これは、四則計算のつまずきの視点と、関連する能力をまとめたものです。どの計算にも、「数理解」「ワーキングメモリ(WM)」「空間認知」の能力が関係していることが分かると思います。
文章題
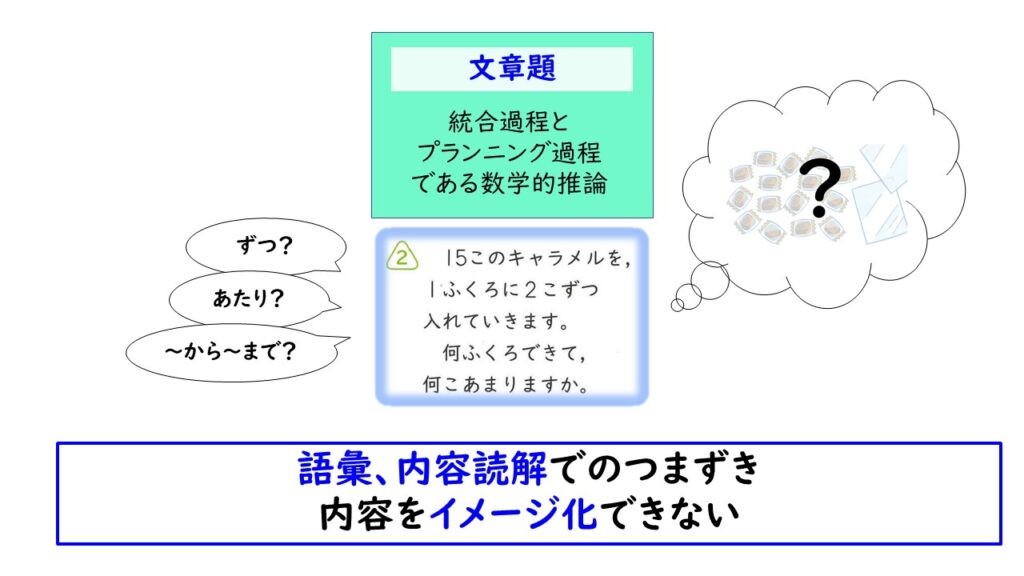
文章題は、また、少し別の視点になります。これは「語彙理解」の問題が大きく関わってきます。
特定のキーワードを捉えて、それを四則計算に何に該当するのかを推測する力に困難を抱えがちとなります。それは、文章を読んでストーリーをイメージする力の弱さと捉えることもできます。
ディスカリキュアは、ディスレクシア・ディスカリキュア(発達性読み書き障害)とも併発する場合が多いので、読みに困難さを抱えていれば、当然、文章題につまずきを抱える場合が多くなります。
その他の「算数」に関連する能力
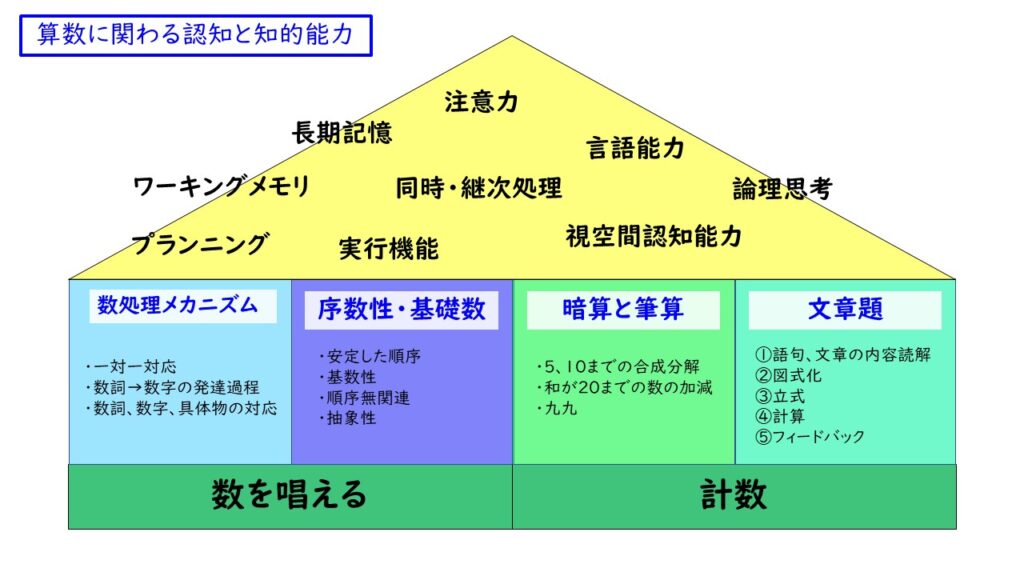
この章では、主たる4つの算数の力を紹介しましたが、算数の力はそれだけではありません。数を数えたり唱えたりする力の上に、「数処理メカニズム」「序数性・基数性」「暗算と計算」「文章題」の4つの力が乗っかります。
さらに、情報を認知したり処理したりする脳の機能が関係してくるのです。答えを導き出すプロセスの全体像を設計し、その通りに進めていく「プランニング」や「実行機能」の能力も当然大きく関わってきます。集中を維持する「注意力」も大切ですし、全体像を捉える方(視覚)が得意なのか、一つ一つ手順を押さえていく方(聴覚)が大事なのかという「同時処理・継次処理」の認知能力も関係してきます。
「ワーキングメモリ」「長期記憶」は記憶保持。「言語能力」や「論理思考」は語彙理解。「どこに何をかくか」という「視空間認知能力」は先に述べた通りです。これらの力を総合して、算数の力と定義されることができます。
算数LDに効果的な指導・支援方法

ここからは様々な指導・支援方法を紹介していきます。全体授業の中で生かす方法、個別に教える上で活用できる方法など、様々です。用途に合わせてカスタマイズしてみてください。
音読/指示

音読や指示は「そんな初歩的なこと」と思ってしまいがちですが、根幹となる支援パーツです。ここを抜かしては、支援の効果は半減するといっても、過言ではないと思っています。
よく見る授業風景では、教師が問題の解き方を解説をします。この解説がLDの子どもにとっては、あまり意味を為さないのが、筆者の経験から言えることです。
説明すればするほど、ディスカリキュアの子どもは混乱します。算数LDの子どもたちは、何が重要な情報で、何が優先順位が高くない情報なのかの、音の選択に困難を抱えています。だから、全体授業であれば、できるだけ言葉を削って、重要な情報しか話さないという教師のスタンスで、丁度バランスがとれるようになります。
具体的には、「教科書20ページ。」(開いたのを確認)「読みます。」(音読させる)「式を教科書に書きます。」(書かせる)、これぐらいの言葉で進めていくのです。「一文で指示」→「作業」のサイクルレベルであれば、ワーキングメモリが少なくても、注意の持続が困難でも、集中を維持することができます。
また、重要な問題は必ず、音読をさせます。もし、文字を見て、意味が全く分からなくても、クラスメイトが音読する音声情報を聞いて、「そういう意味の問題なのか」と入力できる可能性があるからです。このような音声情報の入力方法を工夫・コントロールすることがLDの子どもたちへの支援の根幹となります。
個別で教える場合も、支援者が読んで、その後に音読させたり、「まず何をする?」(○○をする)「15の中に3はいくつある?」(5つある)と一問一答形式で短く聞いて、思考を促してあげることが、ベースとなります。
アルゴリズム
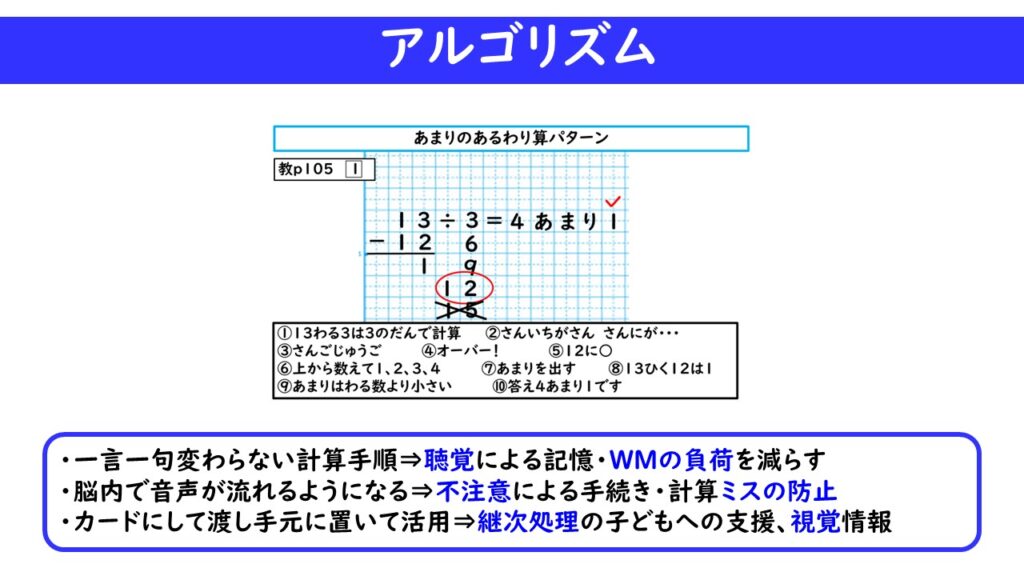
情報を短くするという支援者側の環境を整えた上で、次は、問題の解き方をどのように伝えていくのかが大切です。
授業であれば、黒板に解き方の1ステップを書き、写させる。次の1ステップを書き、写させる。という一つ一つを細分化して進めます。
そして、解き方を口頭でも歌のように唱えさせ、音声情報レベルでもインプットしていくのです。これをアルゴリズムと言います。「この通りにやれば解答を導き出せる」という、固定・確定した手順表だと思ってください。
最初は、教師(支援者)が、アルゴリズムの手順を一つ言い、それを繰り返させます。1日に2~3種類の問題で手順を唱えれば、3日目には、自動的に口から出てくるようになります。毎回アルゴリズムと唱えさせていても、飽きてしまう恐れがあるので、段々と負荷を上げていきます。
例えば、「あまりのあるわり算」では、「まず何の段で計算しますか?」(3の段で計算します)「さんいちが3・・・さんご15・・・どうする?」(オーバー!)「次に何する?」(12に○)のように、答えや次の手順を子ども自身に答えさせていくのです。
そのように、「頼らずに、自分で手順通りできる」という自信を育んでいけばいくほど、スムーズに計算ができるようになっていきます。
また、ワーキングメモリに困難を抱えていたり、聴覚と視覚両方でインプットした方が入るという子どものために、これらのアルゴリズムを前に掲示したり、一覧にして渡しておきます。
単元の始めに「全部で5パターン覚えればこの勉強は全クリなのか」という見通しを持たせて学習させた方が、精神的な負荷も軽くできるからです。参考例として5年生の「小数のわり算」のパターン一覧表を載せておきます。(高学年であればあるほど複雑になっていきますので・・・)
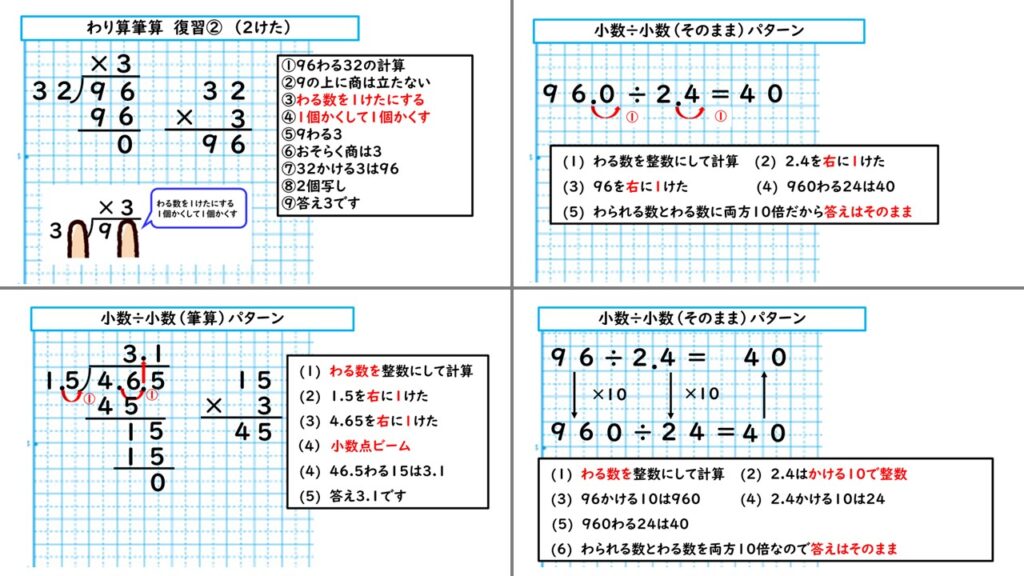
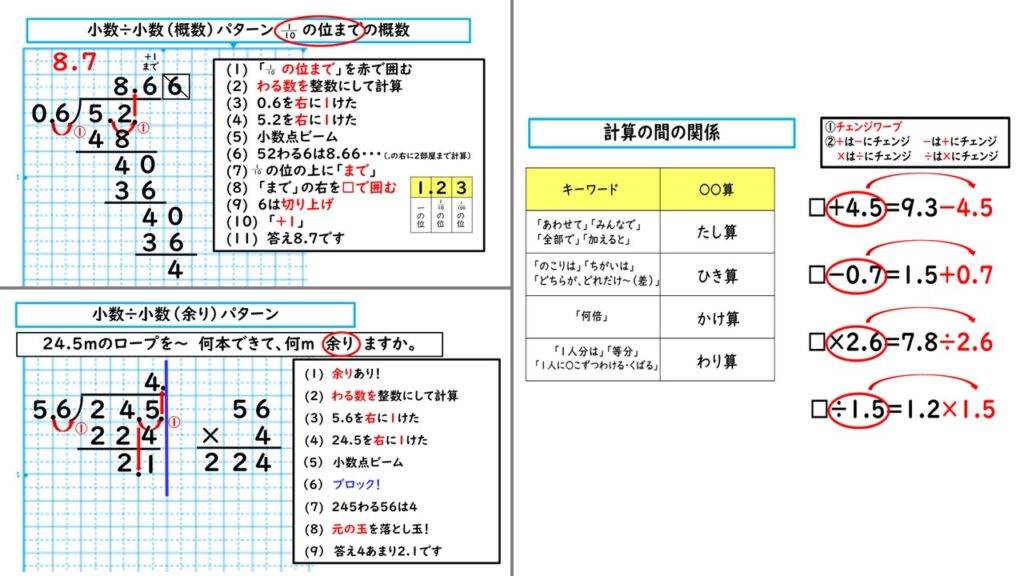
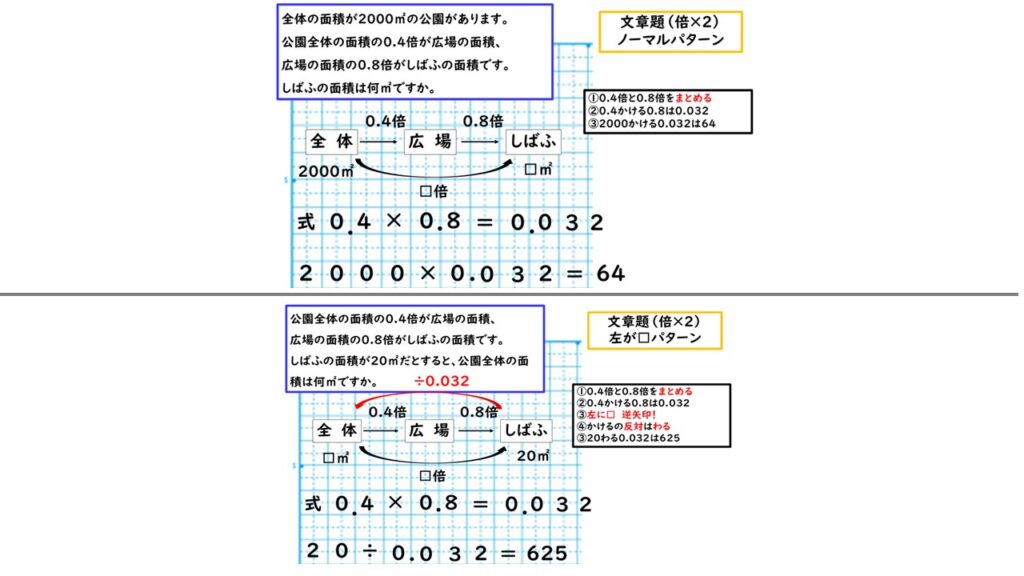
個別に教える場合も、全く同じで、きちんと手順の一つ一つを口に出させていきます。そして「次に何する?」と聞いていき、丁寧に一つ一つの手順を覚えているかどうかを確認しながら進めていくのです。
ノート指導・支援
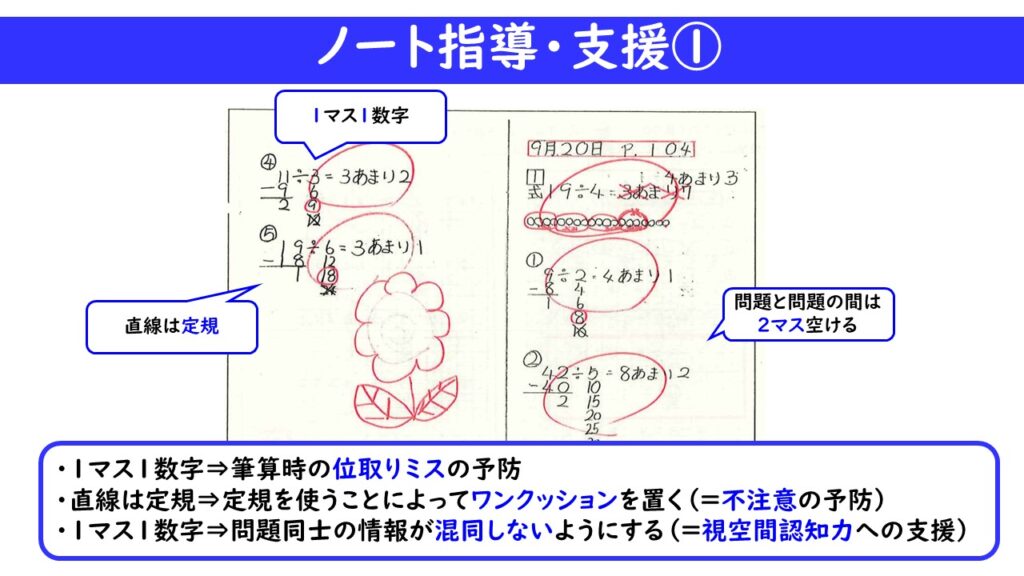

ノートの指導・支援も非常に大切です。ポイントを押さえたノート指導をすれば、平均点が10点は上がると言われているほど、重要ポイントになります。計算ミスが多発する子どもは次のような特徴があります。
・5ミリ方眼の1マスに複数の数字が入ってごちゃまぜになっている
・問題同士を密集してかき過ぎて、問題や答えがどこにあるか分からない
・筆算の線が斜めにかいてあり、整然としたノートになっていない
このような特徴がある子どもは、①の問題を解くのに、②の問題と一部混同してしまったり、筆算の位取りを間違えたりします。
だからこそ、ノート指導を丁寧に行い、1マス1数字にし、問題同士の仕分けがきちんとされている状態にしていくのです。さらに直線は全て定規で引くことによって、速く終わらせようと焦ってミスをするという多動性に対し、ワンクッション置いて、思考を落ち着かせることができます。
また、LDの子どもの中には、板書をノートに写すことに困難を抱える子どもがいます。そのような子どもは、教科書の問題を写すのも一苦労の場合があります。問題を写すことにエネルギーを使ってしまい、解くときにはエネルギーが残っていないとなれば、本末転倒です。
そのような特徴をもつ子どもの場合は、あらかじめこちらがノートに問題をかいておき、本人には解くことに集中してもらうということも重要な支援の一つとなります。
補助計算
次に紹介する「補助計算」も非常に重要な支援です。
これは主にワーキングメモリの負荷を軽くするための支援と捉えてもらって大丈夫です。とにかく「どこまで計算をしたか」「繰り上がりの数は何だったか」といった情報を脳内で留めておくのではなく、ノートに書き記していき、忘れてしまっても、見返すことができるようにしていくのです。

例えば、「あまりのあるわり算」の場合は、三の段を書き記していくことにより、「さんご」がオーバーで、「さんし」の4が答えとなることを忘れずにすみます。答えが4であることをノートに記してあるからこそ、脳の中を空っぽにし、安心してあまりを出す計算に集中することができるのです。
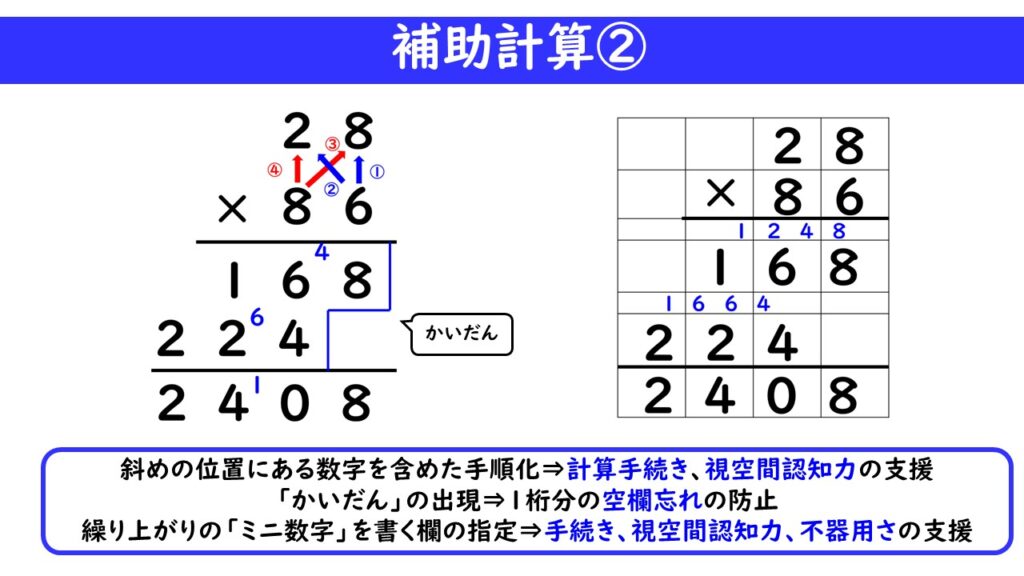
「かけ算筆算」の場合は、どことどこをかけるのかという手順を、こちらが書いておく、もしくは書き込ませるという作業を通して、段々と分かっていくようにすることも支援の一つです。そして、繰り上がりを忘れずに書かせていくことで、計算ミスを減らすことができます。「かいだん」などの空位となる場所を忘れずに空けさせることも大切です。
中には、手先の不器用さや、視空間認知の問題があり、繰り上がりの小さくかく数字と大きい数字が混同してしまう子どももいます。そのような子どもには、繰り上がりをかくスペースをあらかじめつくっておくフレームを使うと本人の負荷を減らすことができます。
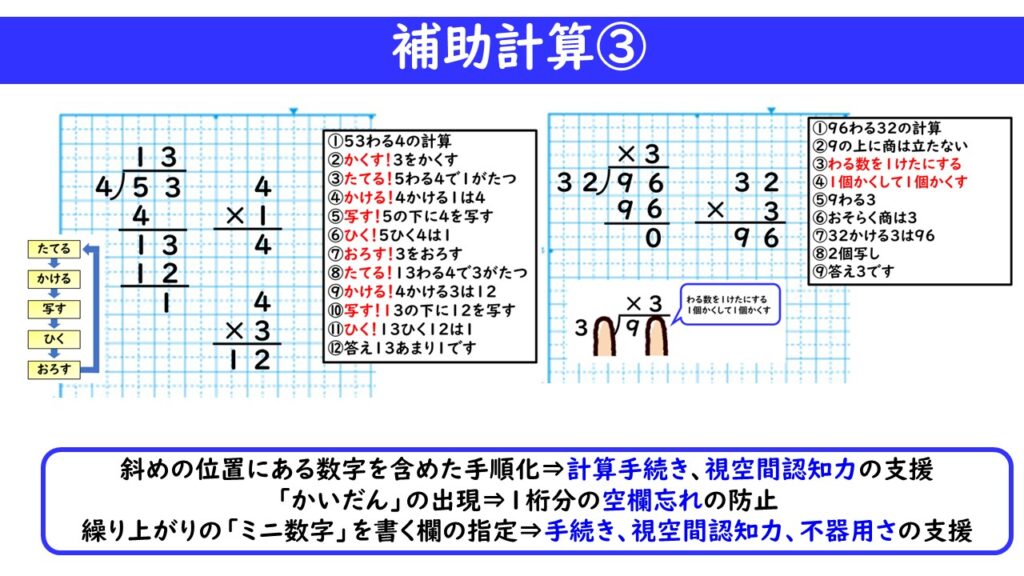
「わり算筆算」であれば、「たてる→かける→(写す)→ひく→おろす」のアルゴリズムを忘れないように掲示しておく、手元に置いておくことが重要です。(ちなみに「写す」は、補助計算を横のスペースにかく場合、それを写すために入れたアルゴリズムです。)
他にも、わり算筆算は、おおよその商の見当をつけることに困難を抱える子どもが多いので、「わる数を一桁にする→1個隠して1個隠す」というように、指で実際に隠して、余分な情報を削り、フォーカスすべき情報に集中させる支援も、とても意味があります。
道具を活用する
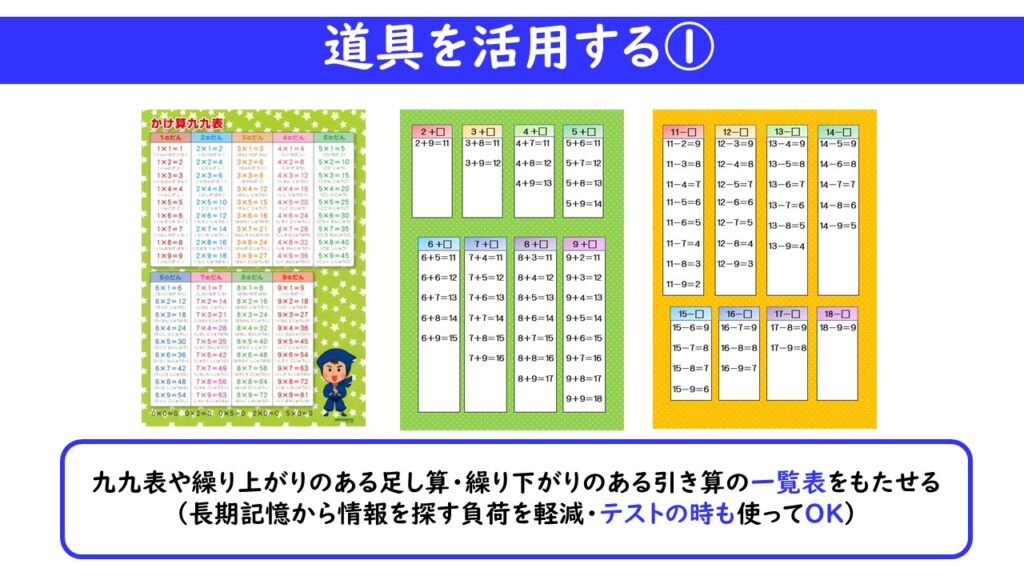
道具を活用することも、超重要事項です。
そもそも九九を覚えていない子どもにとって、かけ算筆算やわり算、わり算筆算を解くことは大変難しいです。その場合は、九九を覚えることに多大なエネルギーを使わせるのでなく、九九表や繰り上がり、繰り下がり表を活用することで、消費エネルギーを節約させるのです。
記憶のメモリが少ないのであれば、外付けのハードディスクを使えばよいのです。筆者は授業中であろうと、テスト中であろうと、このような道具を使ってよいことにしていました。これは、「合理的配慮」と呼ばれ、法律上でも、きちんと認められていることです。(もちろん、九九のテストをするときに九九表は使えませんが・・・)
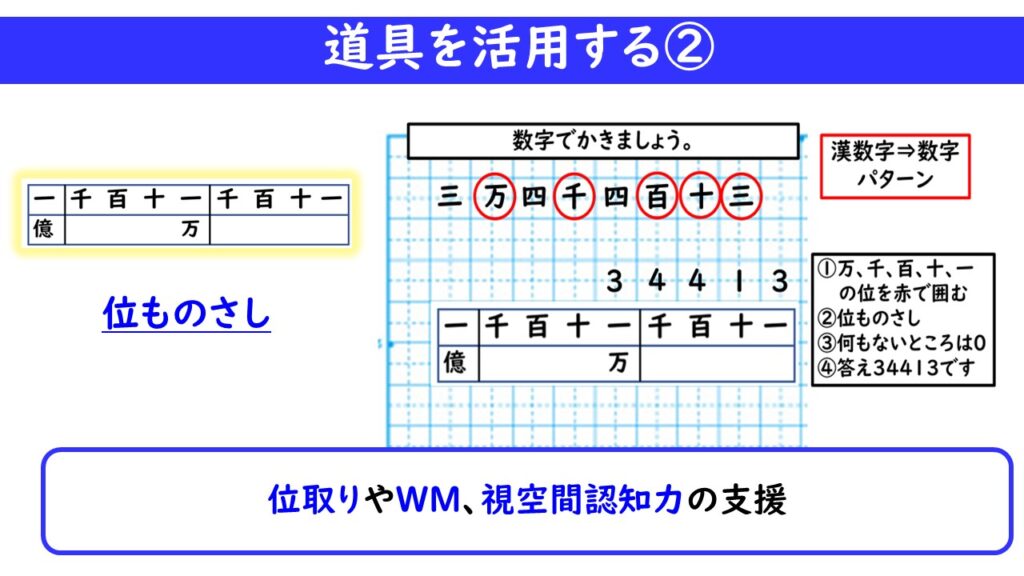
他にも、「大きな数」を学習する際は「位ものさし」を使ったり、様々な単位を習う単元のときは、「単位ものさし」を使ったりしました。これは5ミリ方眼の厚紙をはさみで切って、簡単に作ることができます。
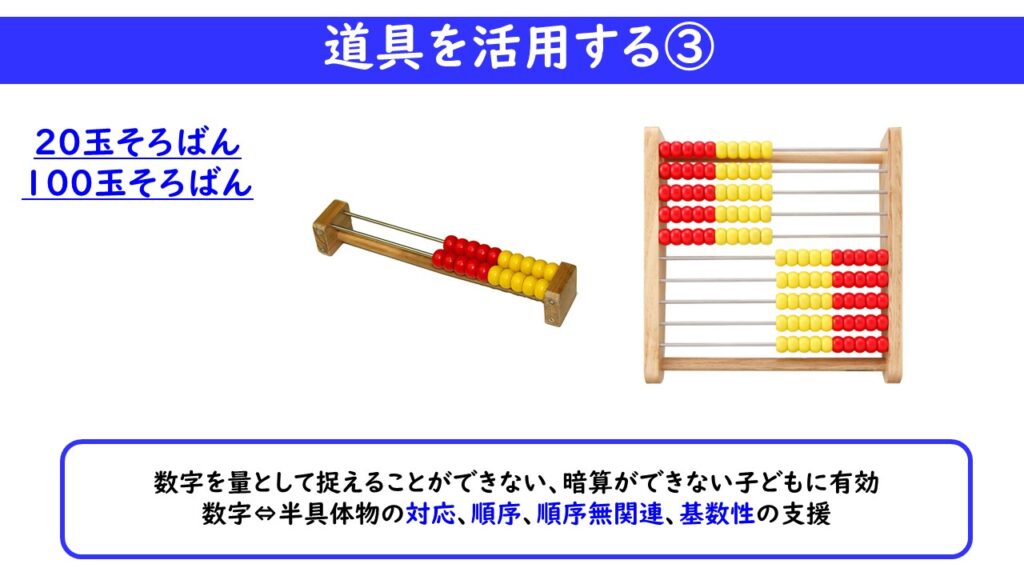

20玉そろばん、100玉そろばんを使った支援もおススメです。
たし算、ひき算に手こずっている子どもには、児童用のそろばんを渡し、計算の補助として使ってよいことにしていました。このそろばんの良いところは、手先が不器用な子どもでも操作がしやすいことと、「量感」を養うことができることです。
「1」は「そろばんの玉1つ分」という数字に対応した量を覚えることができます。この「数処理メカニズム」をどれだけ低学年の内に養っておくかによって、高学年の算数の力が左右されます。
また、授業であれば、教師用の100玉そろばんを、毎授業の冒頭5分を使って指導することは、大変効果があります。
歌のようにリズムよく、みんなで楽しく唱えていく中で、暗算に必要になってくる「10の合成」「10の分解」や、かけ算に必要になってくる「2とび」「5とび」の感覚、そして「どちらが大きい」といった問題を出して「基数性・序数性」の感覚を養うことができます。1日5分を1年間続けたら、間違いなく力が付いていくことでしょう。
文章題の指導
文章題の支援は、「イメージを持たせる」ことと、「キーワードで覚える」こと、「解き方をパターン化する」ことが効果的です。
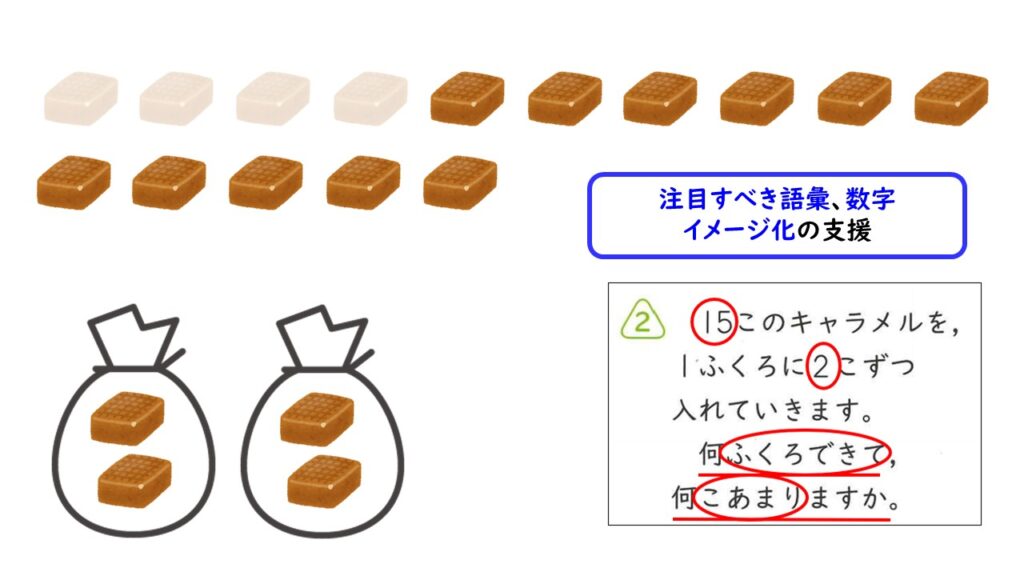
イラストを用いて、どのようなことを聞かれているのかをイメージさせることができます。そうすれば、四則計算の何にあたるのか、見当をつけやすくなるでしょう。

加えて、フォーマットを与えて、一文ごとに文章を読解し、自分でイラスト化や図式化することで、自立して解く力を養っていくことができます。

また、キーワードで何算かを教えてしまうという方法も、シンプルですが、効果があります。自分でイラスト化や図式化がどうしても難しい場合は、このように教えてもOKです。ただ、全ての問題にキーワードが存在するわけではないので、その点は注意が必要です。
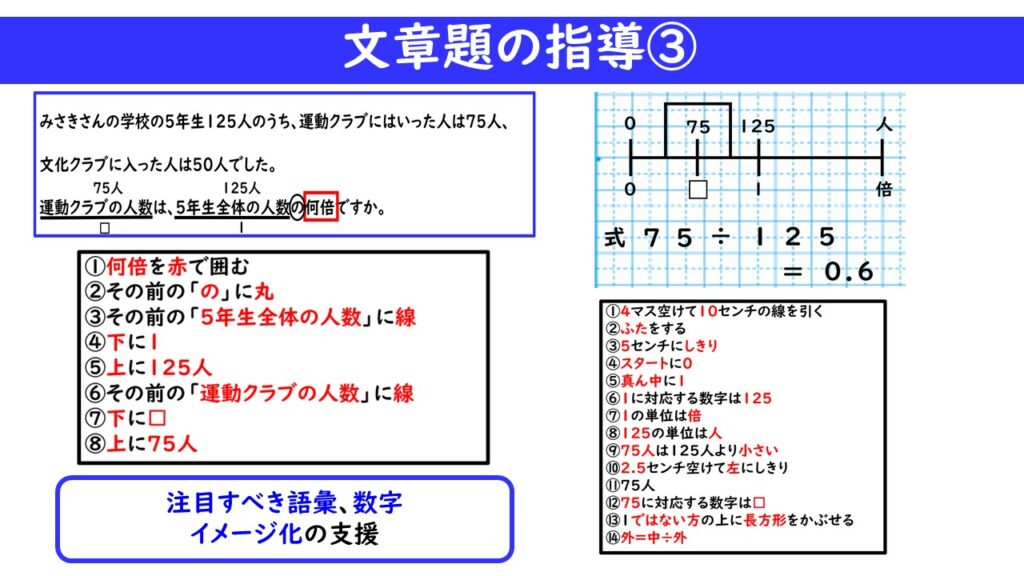
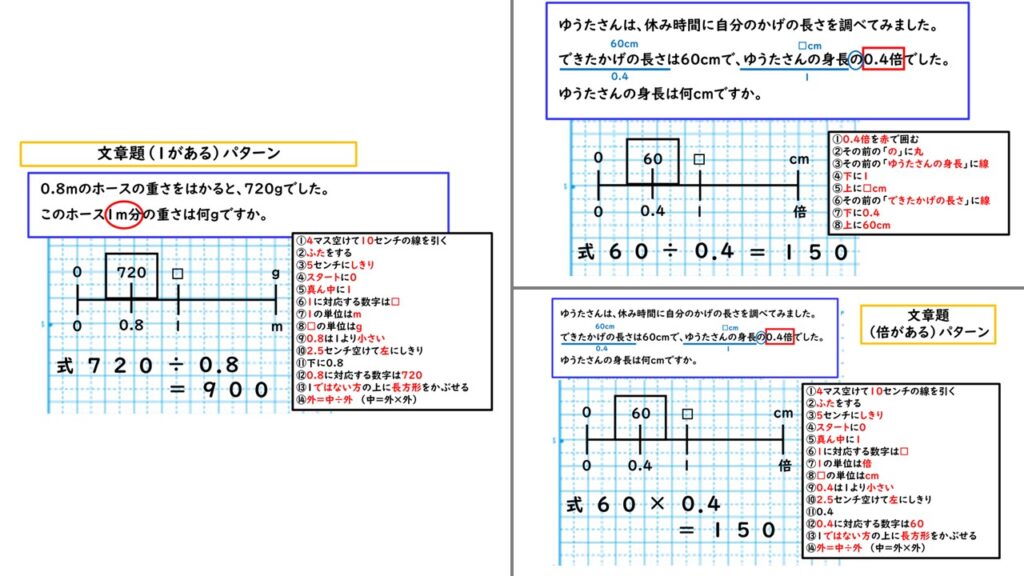
また、5年生の「割合」の単元の問題などは、読んでもわけが分からない場合が多いです。大人が読んでも「意味が分からない」という人が一定数いるのですから、子どもは尚更分からないでしょう。さらに、学習に困難を抱えるLDの子どもにとっては、大混乱を招く可能性も高いです。
そのような場合は、「この問題は、こう解くものだ」という暗記に近い方法で覚えさせていった方が、最終的に成功体験を得て、力を付けていく場合が多いです。上記の数直線を用いた方法では、「小数のかけ算」「小数のわり算」「分数×分数」「分数÷分数」「単位量あたりの計算」「割合」「速さ」「比」など、様々な単元に応用できます。汎用性が高く、使えば使うほど習熟していくので、おススメです。
フラッシュカード

「1km=1000m」のような暗記するしかない学習内容もあります。その場合は、フラッシュカードを用いて、1日2~3分でいいので、パッ、パッとカードを見せて覚えさせた方が、負担を軽減できます。最初は答えが書いてあるカードを見せ、覚えてきたら、答えが隠してあるカードにしていくなどの、徐々に負荷を与えていく工夫は必要です。
まとめ

ここまで様々な指導・支援方法を紹介してきました。これらの方法は、算数LDであろうとなかろうと、算数に苦手意識をもつ子どもにとって効果のある方法ばかりです。もちろん、全ての方法が全員に効果をもたらすわけではありません。
しかし、「なぜ、この子はいつもこの段階でつまずくのだろう?」「なぜ、周囲と比べて計算するスピードに差が出るのだろう?」といった疑問を持ちながら、じっと観察を続けていくと、その子どもが欲している支援が見えてくるはずです。
LDの子どもへの支援はオーダーメイドです。だからこそ、身近な大人が、道を示し、彼ら彼女らの可能性を広げる必要があります。
もちろん、強制するのではなく、「このような方法があるのだけれど、試してみない?」と提案し、進めていく中で、「自分に合った勉強方法はこれなんだ!」と経験させていくことがとても大切になります。よりよい方法を発見するときが低年齢であればあるほど、先の人生で様々な工夫を自分で考え、試行していくことができるでしょう。
この他にも、LD支援の国語編の記事もありますし、様々な教科の教え方や発達の特性の捉え方の記事もあります。多種多様な知見を織り交ぜながら、是非、お子さん・子どもたちへの支援を考えてみてくださればと思います。その他にも何か分からないことがあれば、尋ねてみてください。私に答えられる範囲でお答えできたらと思います。
記事の内容が「よかった」「ためになった」と思われた方は、SNS等にシェアしてくださるとうれしいです。最後まで読んでくださりありがとうございました。








コメント